Circular Motion Problem Set
Follow the Problem Set Instructions & Rubric to complete and submit the following questions:
1. The figure below shows a particle undergoing uniform circular motion at a speed of \( 4.0m/s \).
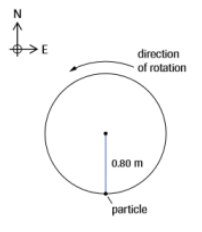
a) State the direction of the velocity vector, the acceleration vector, and the radius vector at the instant shown.
b) Calculate the magnitude of the centripetal acceleration. [Answer: \( 2.0 \times10^1m/s^2 \)]
2. You are whirling a ball on the end of a string in a horizontal circle around your head. What is the effect on the magnitude of the centripetal acceleration of the ball if
a) the speed of the ball remains constant, but the radius of the circle doubles?
b) the radius of the circle remains constant, but the speed doubles?
3. At a distance of \( 25 km \) from the eye of a huricane, the wind is moving at \( 180km/h \) in a circle. What is the magnitude of the centripetal acceleration, in \( m/s^2 \), of the particles that make up the wind? [Answer: \( 0.10m/s^2 \)]
4. Calculate the magnitude of the centripetal acceleration in the following situations:
a) An electron is moving around a nucleus with a speed of \( 2.18 \times10^6 m/s \). [Answer: \( 8.97 \times10^22m/s^2 \)]
b) A cowhand is about to lasso a calf with a rope that is undergoing uniform circular motion. The time for one complete revolution of the rope is \( 1.2s \). The end of the rope is \( 4.3m \) from the centre of the circle. [Answer: \( 1.2 \times10^2m/s^2 \)]
c) A coin is placed flat on a vinyl record, turning at \( 33 \frac{1}{3} rpm \) (revolution per minute). The coin is \( 13cm \) from the centre of the record. [Answer: \( 1.6m/s^2 \)]
5. A ball on a string, moving in a horizontal circle of radius \( 2.0m \), undergoes a centripetal acceleration of magnitude \( 15m/s^2 \). What is the speed of the ball? [Answer: \( 5.5 m/s \)]
6. Mercury orbits the Sun in an approximately circular path, at an average distance of \( 5.79 \times10^{10}m \), with a centripetal acceleration of magnitude \( 4.0 \times10^{-2}m/s^2 \). What is its period of revolution around the Sun, in seconds? in "Earth" days? [Answer: \( 7.6 \times10^6s \) or \( 88 \) Earth days]
7. Let's look at our room on our rotating Earth. We are about \( 45^o \) from the equator. What is our centripetal acceleration? [Answer: \( 0.024m/s^2 \)]

8. Show that \( a_c= \frac{4 \pi^2r }{T^2}=4 \pi^2f^2 \), where T is the period of one rotation in seconds and f is the frequency of rotation in \( Hz \bullet s ^{-1} \).
9. Consider a car going around a curve with a radius of curvature of r and a angle of banking of \( \theta \). If the coefficient of friction between the wheels and the road is \( \mu \), show that the safest speed that the car can go around the track is given as:
\( v=( \frac{ \mu+sin \theta }{cos \theta }rg)^{ \frac{1}{2} } \)