Lesson 5.8 - The Atom
Video is not accessible in some countries. If you cannot view it, you might need VPN to do so.

Position, momentum, energy, and other quantities become probabilities.

Physical phenomenon can now be understood with 'probability amplitudes',
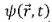 satisfying differential equations, ex. he Schrodinger Equation.
satisfying differential equations, ex. he Schrodinger Equation.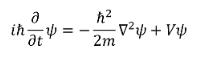
As you can see the mathematics are WAY too difficult for us...
Let's simplify things a little with a "semi-classical" approach to atomic physics.
We can discuss a simplified model of the simplest atom: Hydrogen.
When studying the emission spectra of hydrogen an interesting relationship was discovered.

Any integers, \(n_l\) and \(n_u\), such that \(n_u>n_l\), yielded an emission line with wavelength that followed the relationship.
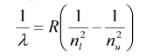
Where R is the Rydberg Constant, R = \(1.097 \times 10^7 m^{-1}\).
WHAT WAVELENGTHS DOES THIS CORRESPOND TO?
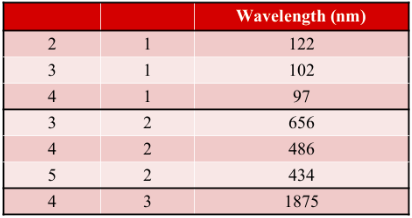
EXAMPLE PROBLEM #1
Calculate the wavelength of light emitted from a hydrogen atom if the electron has a transition from n = 6 to n = 2.SOLUTION:
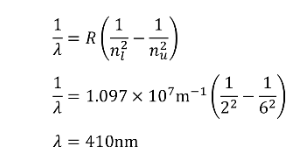
EXAMPLE PROBLEM #2
The hydrogen alpha emission line discussed in the Relativistic Doppler shift has a wavelength of 656nm. What transition caused this photon to be emitted?SOLUTION:
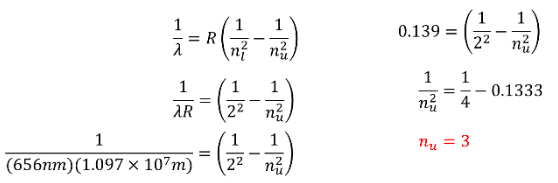
APPLYING WHAT WE KNOW ABOUT A PHOTON'S ENERGY
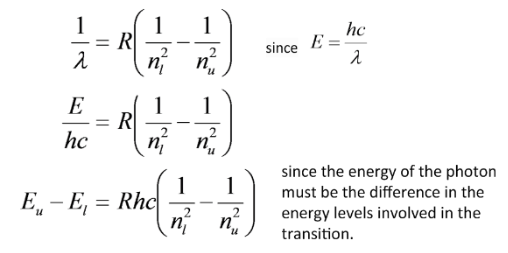
ENERGY LEVELS
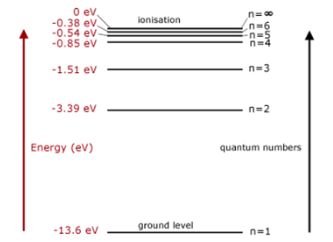
Let's call the state at which n approaches infinity, the ionization state, \(E_I\). Here the electron will gain enough energy to be kicked off of the atom. Then for any energy level, \(E_n\), we can write
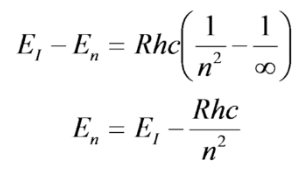
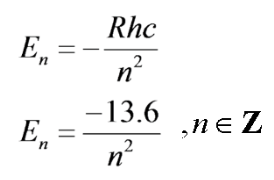
THE BOHR WAVE MODEL OF THE ATOM
We need some way of accounting for the specially allowed energies of an electron that are seen in emission spectra.In 1913, Neils Bohr came up with an idea that electrons can only be allowed around a proton in special orbits equivalent to different energies (Remember grade 9 Chemistry Bohr-Rutherford diagrams)
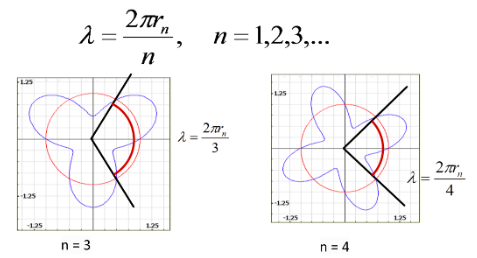
STANDING WAVE MODEL
However, there needed to be some physical justification of these allowable states. Working with the concept of matter waves from deBroglie, Bohr postulated that these states would be allowed if they are vibrating as standing waves around the nucleus at a whole number of the deBroglie wavelength.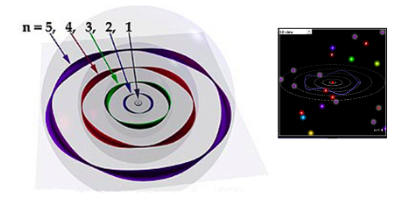
Any other deBroglie wavelengths aren't allowed since they aren't resonant as standing waves around the atom.
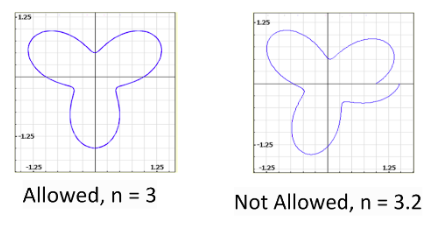
The wavelengths of these standing waves must be integer portion of the total radius.
Recall the deBroglie wavelength
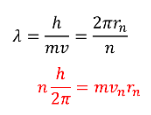
This equation is referred to a Bohr Quantum Condition.
A SEMI-CLASSICAL ANALYSIS OF A HYDROGEN ATOM
If we consider a hydrogen atom as an electron spinning in an orbit, we can use a classical approach to determine some of the characteristics of this "motion" [just remember the uncertainty principle smears everything out]The electron must be held in place by the coulomb force and is "orbiting" with a centripetal force.
Bohr's model gave us our first theoretical approach to an atomic system and allowed us to make some predictions as to the energy and radius of a hydrogen atom.
FAILURES
Unfortunately, the model failed for more complicated atoms. This is because:- It fails to account for the interactions of electrons with other electrons. It works for hydrogen since there is only one electron.
- It only quantizes energy. There is no consideration for the quantization of angular momentum and electron spin
But it does give us a good starting point and a nice theoretical picture of an atom. It was eventually replaced with harder to imagine world of probability densities of Schrondinger and Heisenberg.