[Async-2024-25] SPH4 ...

MATH REVIEW: SIGNIFICANT DIGITS

VIDEO (29:06 min)

Video is not accessible in some countries. If you cannot view it, you might need VPN to do so.

PHYSICS AS AN EMPIRICAL SCIENCE

• Physics is based on a correspondence between measurements and theory.
• Let's think about measurements for a moment.
• All measurements have an inherent uncertainty defined as the measuring device.
• Example: A standard ruler may measure something as being 13.2 cm however there is an uncertainty of \( \pm \) 0.1 cm.
• We need a way to deal with these uncertainties in our calculations.

SIGNIFICANT DIGITS / FIGURES (Sig. figs.)

The following digits are significant: 

• All non-zero digits
• All zeros between non-zeros 
• E.g. 102.05 has 5 sig. figs.
• All zeros left of an understood decimal and right of a non-zero digit 
• E.g. 405 000. has 6 sig. figs.
• All zeros to the right of a decimal point and right of a non-zero digit
• E.g. 0.8050 and 50.00 have 4 sig. figs.

The following digits are not significant:

• All zeros to the right of a decimal point but to the left of a non-zero digit
• E.g. 0.000403 has 3 sig. figs.

CONSTANTS and EXACT NUMBERS

• Significant digits only matter in measurements
• Constants taken from literature and exact numbers have an infinite number of significant digits
• Ex. \( g=9.81 m/s^2 \) and the 2 in the equation \( \Delta t= \sqrt[]{ \frac{2 \Delta d }{g} } \)

OPERAIONS with SIG. DIGS.

• Addition and subtraction: round answer to the least number of digits after the decimal as were provided in the original measurement.

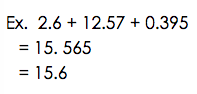
• Multiplication and Division: answer should have the same number of sig. figs. as the measurement with the fewest sig. figs.

SCIENTIFIC NOTATION

Scientific notation is a convenient way of writing numbers of any magnitude and expressing their accuracy by using only sig. figs.

Examples:

• Radius of a hydrogen atom = 0.000 000 000 053 m = 
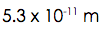
• Radius of Earth = 6 380 000 m = \( 6.38 \times10^6 \) m