Lesson 5.4 - Mass and Energy
VIDEO LESSON (21:52 min)
Video is not accessible in some countries. If you cannot view it, you might need VPN to do so.

Question: So where does this additional mass come from?
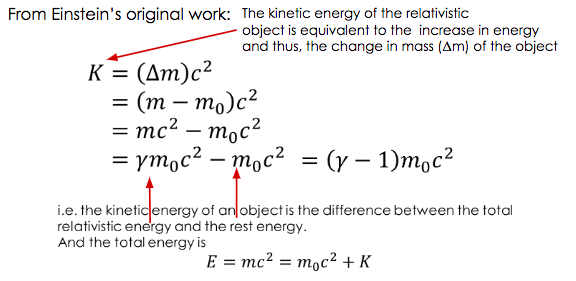

SOLUTION:

To conserve mass-energy, two 511keV gamma rays are produced travelling in opposite directions to conserve momentum.
Video is not accessible in some countries. If you cannot view it, you might need VPN to do so.
SO FAR
Effect of Relativistic speed on a time interval: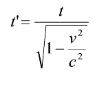
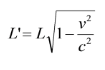
AND ALSO!
Effect of Relativistic speed on a Mass: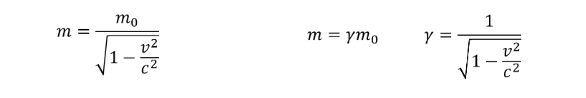
As an object's speed increases, its mass when viewed from a moving frame of reference increases by the factor of \( \gamma \)

RECALL:
Law of Convervation of Mass:
Question: So where does this additional mass come from?
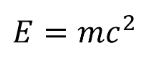
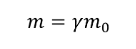
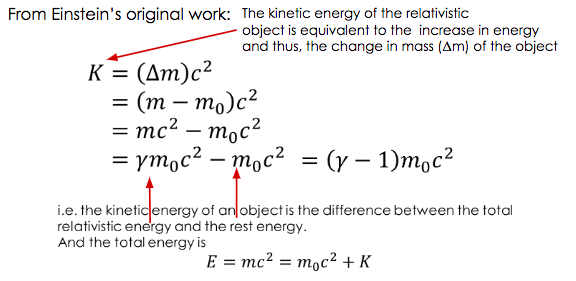

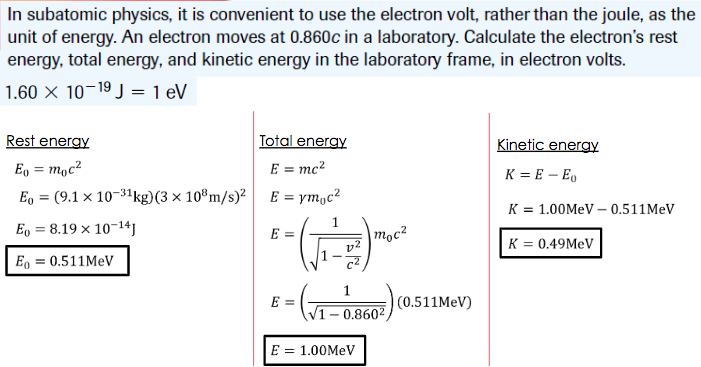
EXAMPLE PROBLEM #1
A neutron has a measured mass of \(1.71 \times 10^{-27} kg\). Determine its speed.SOLUTION:

MASS/ENERGY EQUIVALENCE
Due to the famous equation \(E=mc^2\) we have a precise way of expressing the relationship between rest mass and energy. This is why most subatomic particle masses are listed in \(MeV/c^2\) instead of \(kg\).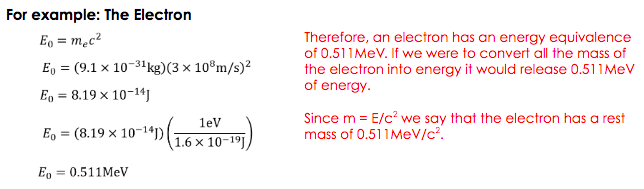
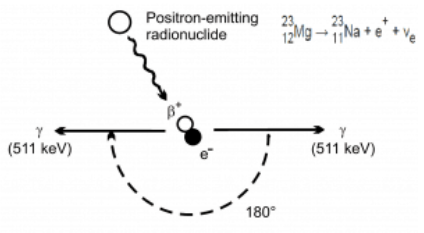
ELECTRON POSITRON ANNIHILATION
After a \( \beta ^+ \) event a positron is produced. After a very short time it interacts with an electron and they annihilate each other (matter-antimatter annihilation).To conserve mass-energy, two 511keV gamma rays are produced travelling in opposite directions to conserve momentum.



EXAMPLE PROBLEM #2
The Large Hadron Collider accelerates protons to 6.8 TeV. How fast are they travelling?
SOLUTION:
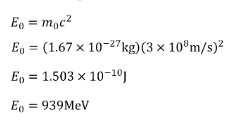
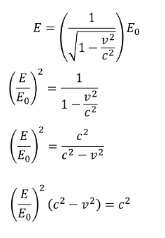
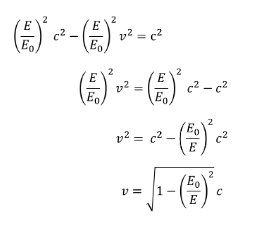

最后修改: 2025年06月28日 星期六 19:36