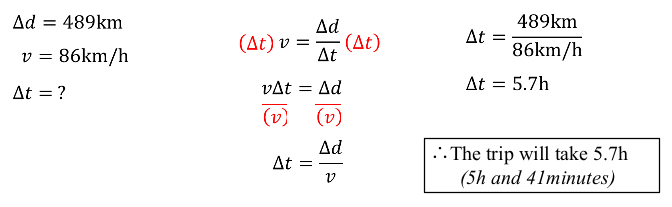Lesson 1.1 - Motion
By the end of this lesson, I will be able to:
- explain the difference between scalar and vector quantities (e.g., distance vs. displacement, speed vs. velocity).
- use correct scientific terminology to describe and communicate motion.
Success Criteria:
By the end of this lesson, I can describe motion clearly and accurately.
I can explain the difference between scalar and vector quantities using examples.
I use correct physics terms like displacement, velocity, and acceleration.
I can distinguish between uniform and non-uniform motion.
Video is not accessible in some countries. If you cannot view it, you might need VPN to do so.
TYPES OF MOTION:
Uniform Motion: Constant speed with constant direction. Examples:
- A plane cruising at a constant speed
- A car with the cruise control down a straight highway
- Walking down a straight hall at constant speed
Non-Uniform Motion: When speed, direction or both are changing. Examples:
- A car slowing down at a stop sign
- A car going around a corner at constant speed
- A tennis ball after being served
SCALAR VS VECTOR QUANTITIES
Scalar: a quantity that has magnitude and no direction.
Should always be written with a symbol, number and units
\(v=15m/s\)
Examples:
- Distance, \( \Delta d\)
- Speed, \(v\)
- Time, \(t\)
- Temperature, \(T\)
- Mass, \(m\)
- Energy, \(E\)
Vector: a quantity that has magnitude and direction. Should always be written with a symbol, numbers, units, and direction.
\( \vec{v} = 15m/s \) [East]
Examples:- Displacement, \( \Delta \vec{d}\)
- Velocity, \( \vec{v}\)
- Force, \(\vec{F}\)
- Acceleration, \( \vec{a}\)
- Momentum, \( \vec{p}\)
SI UNITS
All units we will be using in this course are base of the Systeme International (SI). All units in this system are based on- metre (m)
- kilogram (kg)
- second (s)
All other units are derived from these units. For example
1 Newton = 1 kg m/\(s^2\)
SPEED
Average Speed: Total distance divided by the total time of travel.
\( v_{av}= \frac{ \Delta d }{ \Delta t } \)
Instantaneous Speed: Speed at a particular instant.EXAMPLE PROBLEM #1
A racecar is going around a circular track with a radius of 2.7 km. If it takes \(4.00 \times 10^2 s\) to go around. What is the average speed of the racecar?
SOLUTION:
EXAMPLE PROBLEM #2
The distance from Ottawa to Kitchener is 489 km. If you average a speed of 86 km/h during your trip, How long will it take to drive there?SOLUTION:
