Lesson 3.3 - Electric Potential
VIDEO LESSON (25:57 min)
Video is not accessible in some countries. If you cannot view it, you might need VPN to do so.

We can now broaden this definition to any electric field, not just one confined to a conductor.
We have an equation of the electric potential energy of bringing a charge \(q_2\) from infinity to a distance r away from a charge \(q_1\).

SOLUTION:
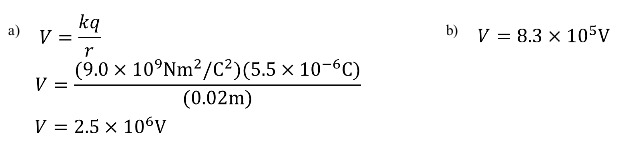
SOLUTION:
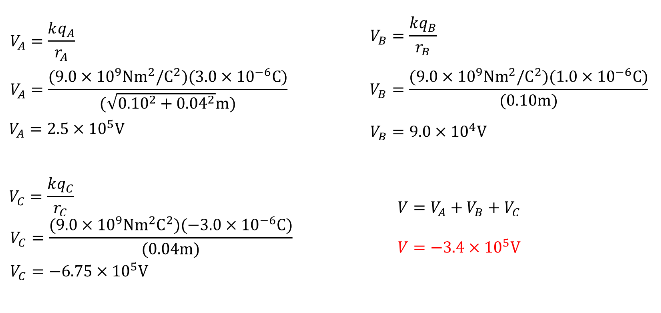
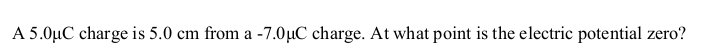
SOLUTION:
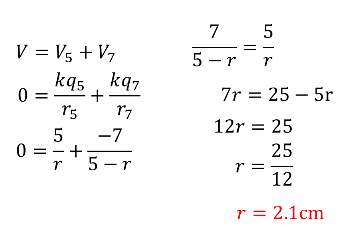
Video is not accessible in some countries. If you cannot view it, you might need VPN to do so.
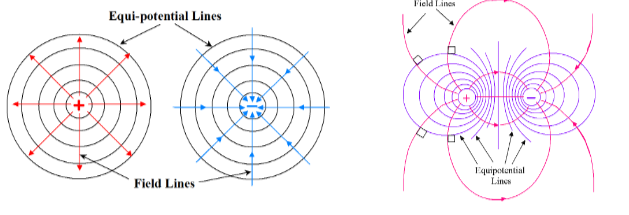
RECALL: GRAVITY
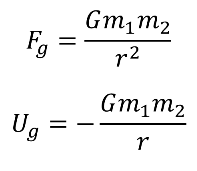
ELECTRICAL VS GRAVITY
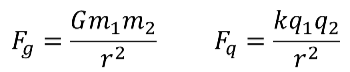
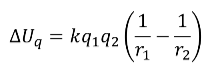
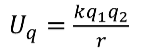

LET'S GO BACK TO GRADE 9
We used a term electric potential difference when referring to the change in potential energy of a unit charge, across a portion of a circuit. It was also called voltage [measured in J/C].We can now broaden this definition to any electric field, not just one confined to a conductor.
We have an equation of the electric potential energy of bringing a charge \(q_2\) from infinity to a distance r away from a charge \(q_1\).
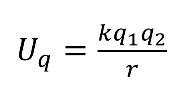
VOLTAGE
If we define V to be the change in potential of a unit charge and consider \(q_2\) to be the unit charge.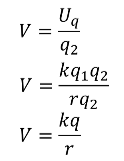
This defines the Electrical potential difference. Note that this is a scalar.
EXAMPLE PROBLEM #1

SOLUTION:
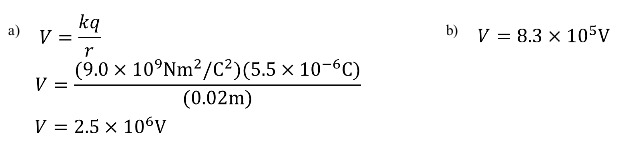
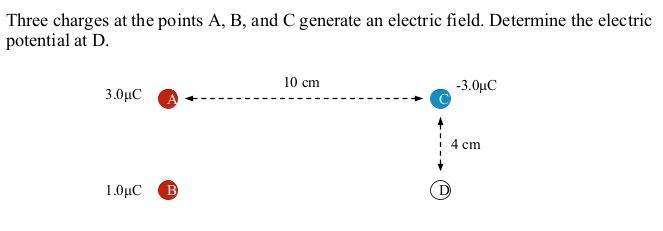
EXAMPLE PROBLEM #2

SOLUTION:
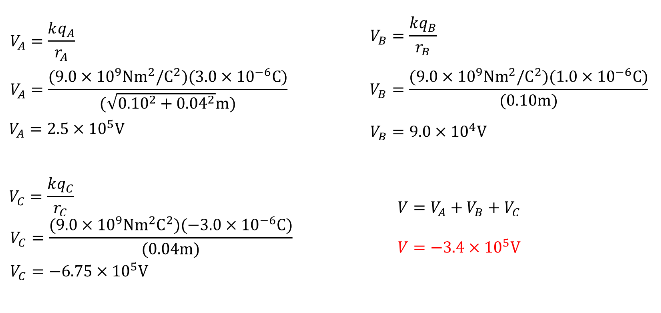
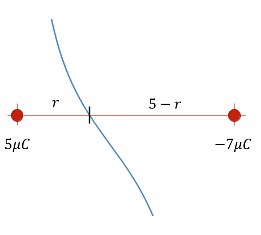
EXAMPLE PROBLEM #3
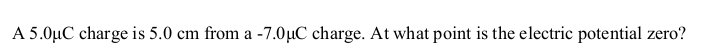

SOLUTION:
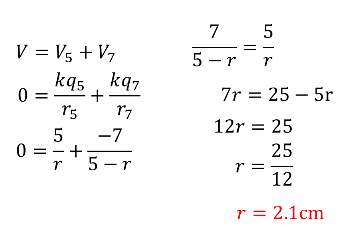
EQUIPOTENTIAL LINES
We can generate lines that represent a surface where the potentials are the same. They are at right angles to the field lines.
最后修改: 2025年06月19日 星期四 16:35