Lesson 3.8 - Ampere's Law and Faraday's Law
VIDEO LESSON (28:50 min)
Video is not accessible in some countries. If you cannot view it, you might need VPN to do so.
Ampere's Law: how a current creates a magnetic field
Faraday's Law: how a magnetic field creates a current
These two laws have a natural symmetry to them that hints of the underlying nature of electromagnetism

SOLUTION:
\( B= \frac{\mu_o I}{2 \pi r} \)
\( B= \frac{(4 \pi \times 10^{-7}Tm/A)(3.0 \times 10^5 A)}{2 \pi (0.15m)} \)
\( B=0.40\) T
SOLUTION:
\( B= \frac{\mu_o NI}{L} \)
\( B= \frac{(4 \pi \times 10^{-7}Tm/A)(400)(10 A)}{2 \pi (0.20m)} \)
\( B=0.025T\) or 25 mT
The direction of the current is such that the magnetic field it produces opposes the change that produced it (Lenz's Law).
This is a product of the Law of conservation of energy. The energy gained by the current is lost by the magnet.


Video is not accessible in some countries. If you cannot view it, you might need VPN to do so.
ELECTROMAGNETISM
Interaction between Electricity and Magnetism:Ampere's Law: how a current creates a magnetic field
Faraday's Law: how a magnetic field creates a current
These two laws have a natural symmetry to them that hints of the underlying nature of electromagnetism
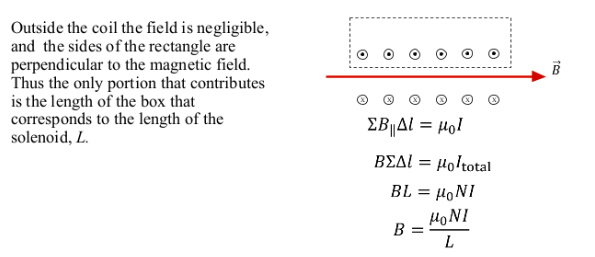
AMPERE'S LAW
Consider a uniform magnetic field perpendicular to a plane.
Consider a closed path, \(l\), through the magnetic field. The shape is arbitrary but closed

Where:
\(B_{||}\) is the component of the magnetic field parallel to the path \(\Delta l\)
\( \mu_o \) is the permeability of free space \( 4 \pi \times 10^{-7} \) Tm/A
EXAMPLE
Consider a straight wire carrying a current, \(I\), through it and for simplicity, let's consider a circular path around the wire with a radius, \(r\).
EXAMPLE PROBLEM #1
What is the magnetic field strength 15cm from a straight wire with \(3.0 \times 10^5\) A flowing through it?SOLUTION:
\( B= \frac{\mu_o I}{2 \pi r} \)
\( B= \frac{(4 \pi \times 10^{-7}Tm/A)(3.0 \times 10^5 A)}{2 \pi (0.15m)} \)
\( B=0.40\) T
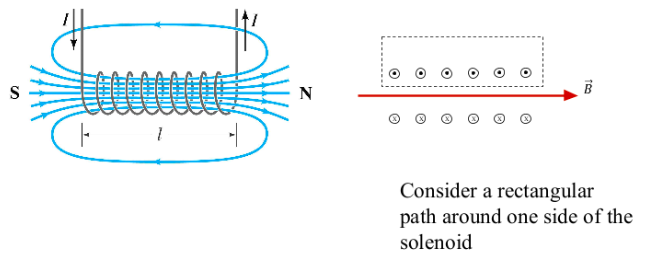
WHAT ABOUT A SOLENOID?


EXAMPLE PROBLEM #2
Determine the magnetic field in a solenoid carrying a current of 10A. It consists of 400 turns of copper wire over a length of 20cm.SOLUTION:
\( B= \frac{\mu_o NI}{L} \)
\( B= \frac{(4 \pi \times 10^{-7}Tm/A)(400)(10 A)}{2 \pi (0.20m)} \)
\( B=0.025T\) or 25 mT
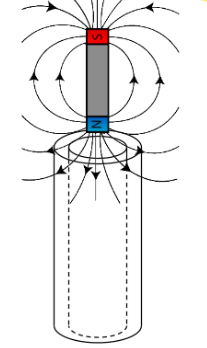
FARADAY'S LAW
A magnetic field changing as a function time induces a current.The direction of the current is such that the magnetic field it produces opposes the change that produced it (Lenz's Law).
This is a product of the Law of conservation of energy. The energy gained by the current is lost by the magnet.



IN SUMMARY: MAXWELL'S EQUATIONS
Sửa lần cuối: Thứ sáu, 20 Tháng 6 2025, 10:28 PM
