Lesson 5.5 - The Quantum Problem
Video is not accessible in some countries. If you cannot view it, you might need VPN to do so.
NEXT PROBLEM: BLACKBODY RADIATION
When an object that is heated up gives off light and the distribution of wavelengths of that light has a distinctive curve: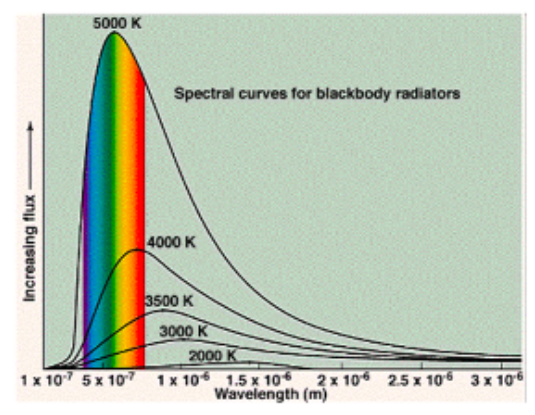
We call this a Boltzmann curve.
MAX PLANCK

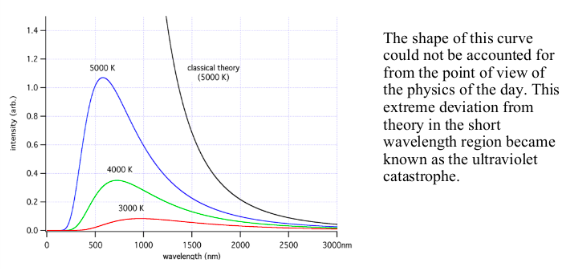
German physicist Max Planck was able to empirically fit the blackbody curve by using a trick from statistical mechanics whereby the energy a particle has must be a multiple of a smallest piece of energy. Energy is radiated in packets called quanta.
Empirically: Based on experimental results, not necessarily bound to theoretical restraints.
He proposed that the energy of a single quanta is directly proportional to the frequency of radiation.
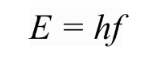
Where E is the energy in Joules (J), f is the frequency in hertz (Hz) and h is Planck's Constant (\(6.63 \times 10^{-34} Js\)).
This means energy can only come in discrete, quantized amounts.
How much energy does red light (650nm) have? Answer in Joules (J) and Electronvolt (eV)
SOLUTION:
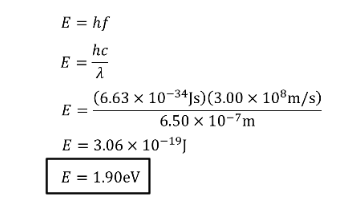
PHOTOELECTRIC EFFECT
When light would shine on a metal, electrons would be released.Main Result
The kinetic energy of the released electrons in proportional to the frequency of incident light and below a threshold frequency no electrons are released.
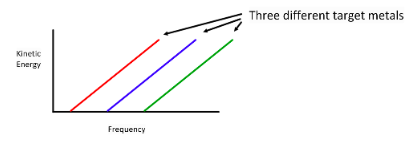
It turns out the slope of the lines in Planck's Constant.
Thus, the kinetic energy of the ejected electrons is
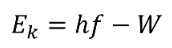
\(E_k\) The kinetic energy of the ejected electron (J or eV)
\(h\) Planck's Constant (\(6.63 \times 10^{-34} Js\) or \(4.14 \times 10^{-15} eVs\)) 1eV = \(1.602 \times 10^{-19} J\)
\(f\) Frequency of incident light (Hz)
\(W\) Work function of the target material (J or eV) [energy required to remove an electron]
EXAMPLE PROBLEM #2
What wavelength of light is required to eject electrons from Tungsten (W=4.52eV) if the maximum kinetic energy of the electrons is 1.68eV.
SOLUTION:
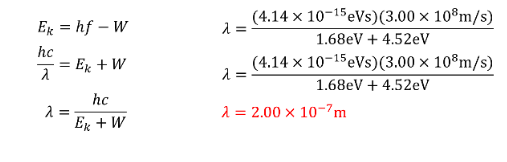
BUT WAIT...
If we use Planck's Equation of quantized energy, then we have to accept that light is also quantized. Thus light comes in discrete packets or photons.
Hmmm...Let's look at another experiment.
COMPTON SCATTERING
Similar to the Photoelectric effect but instead of visible light, high energy X-rays are used. What Compton found was that electrons where still ejected BUT at an angle and lower energy X-rays were also detected.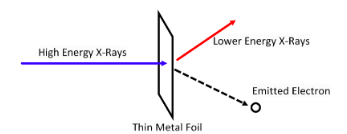
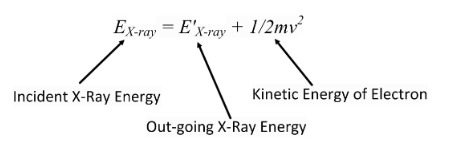
Compton showed experimentally that this was the case.
WHAT ABOUT MOMENTUM?
If the electron leaves with some velocity (and at an angle), and we consider the X-ray strike as a collision, then the incident X-ray had to have some momentum for the Law of Conservation of Momentum to still be valid.But how can a proton have momentum?
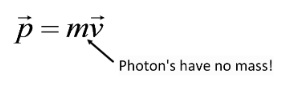
However, Einstein tells us that mass and energy have an equivalence relation
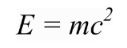
So the X-ray has a mass equivalence of 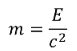
So...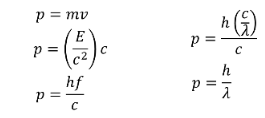
MOMENTUM (EQUIVALENCE) OF A PHOTON

So not only is light made up of packets of light with energy hf, it has momentum, which is definitely particle-like behaviour.
So how is it possible to have particle-like behaviour AND wave-like behaviour?
Quick answer: A photon is a wave packet