Lesson 5.7 - Uncertainty
Video is not accessible in some countries. If you cannot view it, you might need VPN to do so.
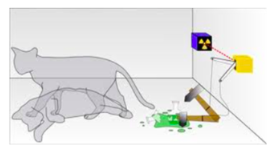
SCHRODINGER'S CAT
You may have heard of the following thought experiment first considered by Erwin Schrodinger.
Consider a cat in a box. We can't see in the box, hear what's going on in box or observe it in anyway. Also inside the box is a poison vial connected to an apparatus that will break open the vial in the event that a radioactive-particle will decay.
Is the cat alive or dead?

According to the Copenhagen Interpretation of quantum mechanics, we say that while the box is closed it is in a superpositon of the two states: live and dead. When we open the box this superposition collapses into one of either staes: live or dead. Whether or not it is alive or dead becomes a probability problem.
THE CENTRAL TENET OF QUANTUM MECHANICS

CONSIDER AN ATOM
To determine its position lets reflect light off of it.
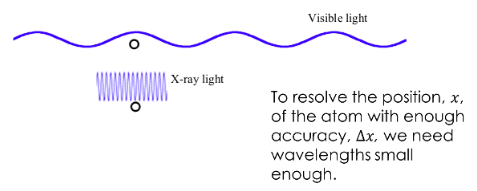
However, once we decrease the wavelength the momentum of the photon increases. To accurately resolve atoms we need light in the x-ray regions and these photon have a lot of energy.
The collision between the photon and the atom will impart a velocity on the atom and it will move and we now lose track of its momentum!
It is impossible to measure the position and momentum of an object simultaneously with infinite accuracy. In observing one we disturb the other.
In 1927, Werner Heisenberg showed that there is a precise mathematic expression for uncertainty of the simultaneous measurement of position and momentum:
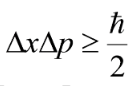
The uncertainty in the position and the momentum are inversely proportional.
CAREFUL!
This has nothing to do with the accuracy of our instruments but the indeterminacy of the simultaneous observables. It is a physical limit on the most accurate measurement possible.
EXAMPLE PROBLEM #1
The position of a baseball is measured to an accuracy of \(10^{-4}m\). What is the minimum uncertainty possible for a measurement of velocity. \(M_{baseball}=160g\)SOLUTION:
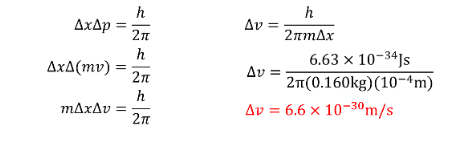
EXAMPLE PROBLEM #2
Determine the minimum uncertainty in the measurement of velocity of an electron if the position is measured an uncertainty of a) \(10^{-4}m\)
b) \(10^{-10}m\)
SOLUTION:
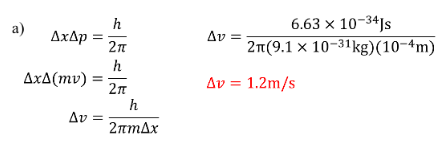
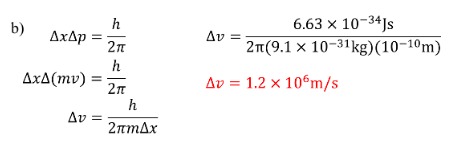
We can now answer our last problem from the beginning of the unit:

From a classical electrostatic view the potential energy of a positive and a negative charge varies as an inverse of the position.
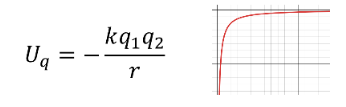
So the charges would want to get closer and closer to each other to reduce the potential energy between reaching a lowest point when they crash into each other.
BUT!!!
To reduce the distance between the electron and the proton we need to constrain its position and thus reduce the uncertainty in its position. But due to the Uncertainty principle this will increase the uncertainty in the momentum of the electron.Again this isn't just the uncertainty in how we measure it. The electron will actually behave more erratically and 'wiggle' more increasing its kinetic energy!
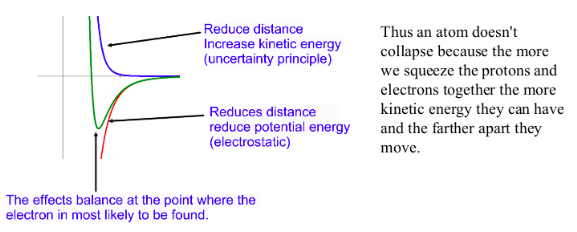
DETERMINISM VS PROBABILITY
In Newtonian mechanics it is possible to propose that is we were able to find all the positions and velocities of every particle in the universe we could predict every aspect of the future. We call this Determinism.The Heisenberg's Uncertainty principle now tells us this view of the world is flawed since we can't know all this information precisely.
The only way that we can understand or predict the behaviour of a quantum mechanical system is through probabilities. We assign a probability to an event or observable
ATOMS BEFORE QUANTUM MECHANICS
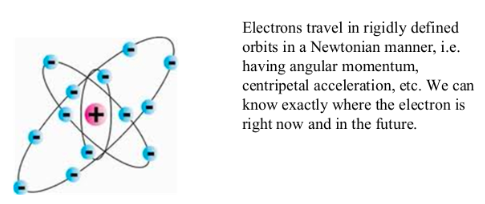
THE REVISED ATOM