Derivatives Unit Test - Breakdown & Review Guide
TEST FORMAT
REVIEW GUIDELINES
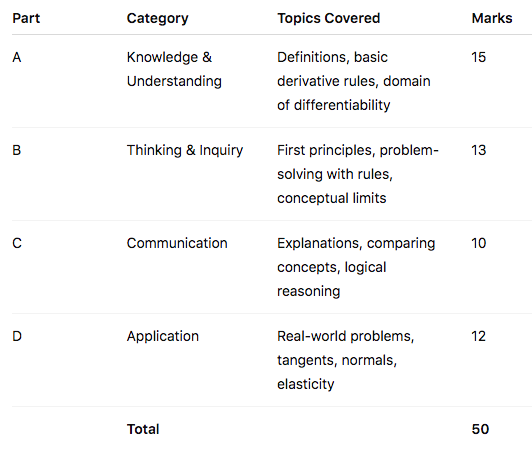
Part A: Knowledge & Understanding (15 marks)
Topics:
- Definition of derivative from first principles
- Power, product, quotient, and constant rules
- Domains of differentiability (e.g., square roots, absolute value)
Practice:
- Memorize the first principles definition:
\( f'(a) = \lim_{h \to 0} \frac{f(a+h) - f(a)}{h} \)
- Practice simple derivatives: \( x^n \), constants, and basic sums.
- Be able to determine where a function is not differentiable (e.g., at cusps, corners, or discontinuities).
Part B: Thinking & Inquiry (13 marks)
Topics:
- Use of first principles to find a derivative.
- Find horizontal tangents by solving \( f'(x) = 0 \).
- Justifying non-differentiability with one-sided limits.
- Interpreting velocity from position functions.
Practice:
- Fully work out at least 2-3 first-principles problems from scratch.
- Solve polynomial derivative problems and identify horizontal tangents.
- Review limit-based reasoning, especially with absolute value.
Part C: Communication (10 marks)
Topics:
- Explaining the difference between instantaneous and average rate of change.
- Relationship between continuity and differentiability.
- Clear explanation of finding a tangent line using steps.
Practice:
- Be ready to clearly explain key concepts in your own words.
- Use examples from real life (e.g., driving speed vs. average speed).
- Review how to write equations of lines from points and slopes.
Part D: Application (12 marks)
Topics:
- Motion applications (velocity = derivative of position)
- Normal lines (perpendicular to tangents)
- Elasticity of demand from real-world examples
Practice:
- Know how to:
- Differentiate position functions and intepret velocity
- Find and interpret the slope of a tangent or normal line
- Use \( E= \frac{p}{n(p)} \cdot n'(p) \) to discuss elasticity
Modifié le: jeudi 22 mai 2025, 14:23