Lesson 1.5 - Orbital Dynamics
VIDEO LESSON (42:33 min)
Video is not accessible in some countries. If you cannot view it, you might need VPN to do so.
Both objects are rotating about their central mass (barycenter).
Can you show diagrammatically that a force directed along the line between the centres of the Sun and a planet would cause the planet's speed to increase as it approached the Sun and decrease as it moved away? If you can, you have demonstrated that Kepler's second law supports Newton's proposed law of universal gravitation.
Problem
How does a force that follows an inverse square relationship affet the orbital speed of a planet in an elliptical orbit?
Equipment

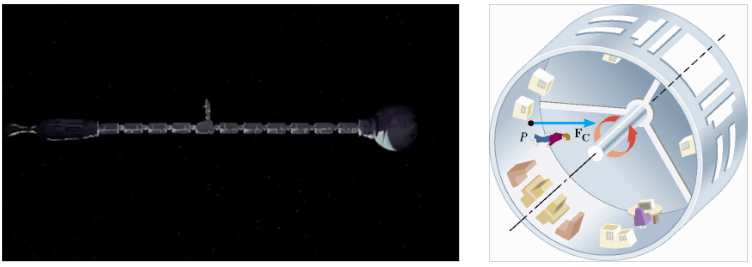
How fast is the ring spinning on the Discovery One? It has a radius of \( 6.0 m \) and let's assume that it generated a gravitational field of \( 1.6 m/s^2 \).
SOLUTION:
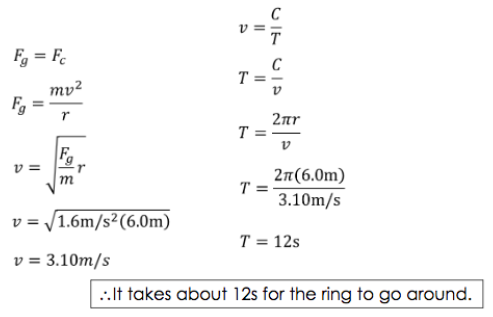


The Coriolis force is the reason that weather patterns always rotate the same direction in each hemisphere.

Video is not accessible in some countries. If you cannot view it, you might need VPN to do so.
ORBITAL DYNAMICS
- Orbit shapes and speeds
- Lagrangian points
- Geostationary orbits
- Artificial Gravity
- Coriolis Effect
KEPLER'S 1ST LAW
The orbits of planets are ellipses where the central mass is located at one of the foci of the ellipse.
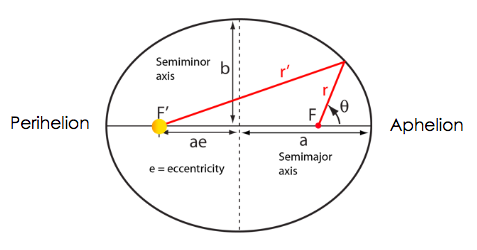
Both objects are rotating about their central mass (barycenter).
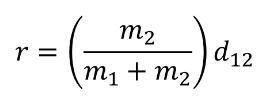
Can you show diagrammatically that a force directed along the line between the centres of the Sun and a planet would cause the planet's speed to increase as it approached the Sun and decrease as it moved away? If you can, you have demonstrated that Kepler's second law supports Newton's proposed law of universal gravitation.
Problem
How does a force that follows an inverse square relationship affet the orbital speed of a planet in an elliptical orbit?
Equipment
- corkboard or large, thick piece of cardboard
- 2 pushpins
- blank paper
- 30 cm loop of string
- pencil
- ruler
- Place the paper on the corkboard or cardboard. Insert two pushpins into the paper about 8 to 10 cm apart.
- Loop the string around the pushpins, as shown in the illustration. With your pencil, pull the string so that it is taut and draw an ellipse by pulling the string all the way around the pushpins.
- Remove the string and pushpins and label one of the pinholes "Sun".
- Choose a direction around the elliptical orbit in which your planet will be moving. Make about four small arrowheads on the ellipse to indicate the direction of motion of the planet.
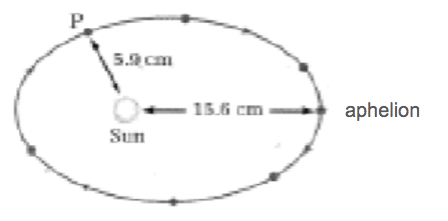
- Make a dot for the planet at the point that is most distant from the Sun (the perihelion). Measure and record the distance on the paper from the perihelion to the Sun. From that point, draw a 1 cm vector directed straght toward the Sun.
- This vector represents the force of gravity on the planet at that point: \( F_{g(peri)} = 1 unit \). (\( F_{g(peri)} \) is the force of gravity when the planet is at perihelion.)
- Select and label at least three more points on each side of the ellipse at which you will analyze the force and motion of the planet.
- For each point, measure and record, on a separate piece of paper, the distance from the Sun to point P, as indicated in the diagram. Do not write on your diagram, because it will become too cluttered.
- Follow the steps in below to see how to determine the length of the force vector at each point.
- The masses of the Sun and planet remain the same, so the value \( Gm_Sm_P \), is constant. Therefore, the expression \( F_gr^2 \) for any point on the orbit is equal to the same value.
- \( F_g=G \frac{m_Sm_P}{r^2} \)
- \( F_gr^2=Gm_Sm_P \)
- Consequently, you can set the expression \( F_gr^2 \) for any one point equal to \( F_gr^2 \) for any other point. Use the values at perihelion as a reference and set \( F_{g(P)}r^2 \) equal to \( F_{g(peri)}r^2_{peri} \). Then solve for the \( F_{g(P)} \).
- \( F_{g(peri)}r^2_{peri}=F_{g(P)}r^2_P \)
- \( F_{g(P)}= \frac{F_{g(peri)}r^2_{peri}}{r^2_P} \)
- You can now find the relative magnitude of the gravitational force on the planet at any point on the orbit by substituting the magnitudes of the radii into the above equation. For example, the magnitude of the force at point P in step 8 is 6.99 units.
- \( F_{g(P)}= \frac{(1 unit)(15.6cm)^2}{(5.9 cm)^2} \)
- \( F_{g(P)}=6.99 units \)
- Calculate the length of the force vector from each of the points that you have selected on your orbit.
- On your diagram, draw force vectors from each point directly toward the Sun, making the lengths of the vectors equal to the values that you calculated in step 10.
- At each point at which you have a force vector, draw a very light pencil line tangent to the elipse. Then, draw a line that is perpendicular (normal) to the tangent line.
- Graphically draw components of the force vector along the tangent (\( F_T \)) and normal (\( F_N \)) lines, as shown in the diagram.
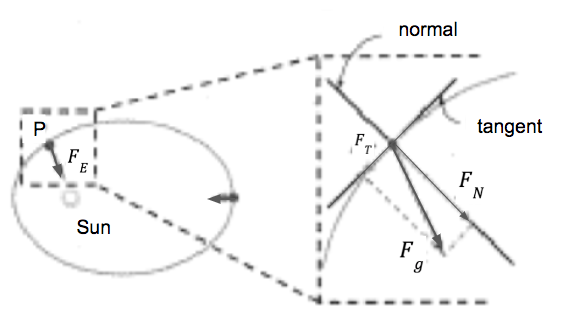
- The tangential component of the force vector (\( F_T \)) is parallel to the direction of the velocity of the planet when it passes point P. What effect will the tangential component of force have on the speed of the planet?
- The normal component of the force vector (\( F_N \)) is perpendicular to the direction of the velocity of the planet when it passes point P. What effect will the normal component of force have on the velocity of the planet?
- Analyze the change in the motion of the planet caused by the tangential and normal components of the gravitational force at each point where you have drawn force vectors. Be sure to note the direction of the velocity of the planet as you analyze the effect of the components of force at each point.
- Summarize the changes in the velocity of the planet as it makes one complete orbit around the Sun.
- The force vectors and components that you drew were predictions based on Newton's Law of Universal Gravitation. How well do these predictions agree with Kepler's observations as summarized in his second law? Would you say that Kepler's data supports Newton's predictions?
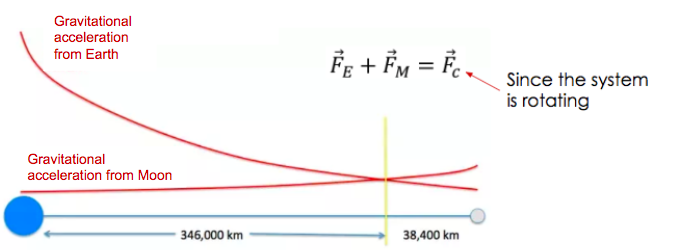
CONSIDER THE GRAVITATIONAL FORCE ON A BODY BETWEEN EARTH AND THE MOON
CONSIDER THE ASTEROID BELT
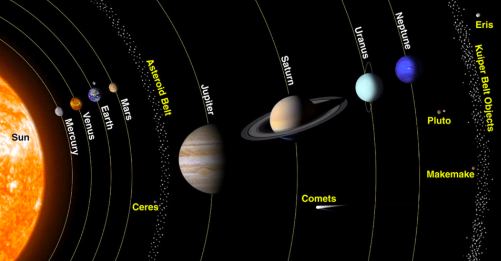
WHY DOES THE TROJAN ASTEROID GROUP EXIST?
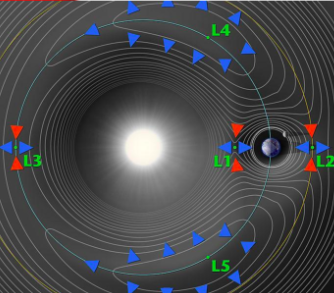
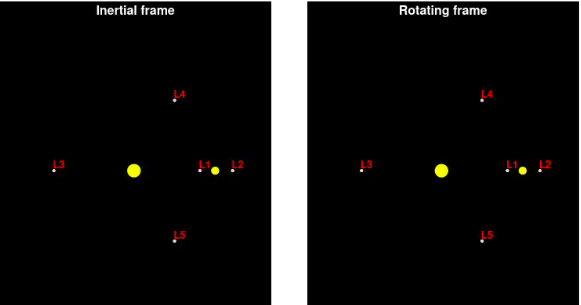
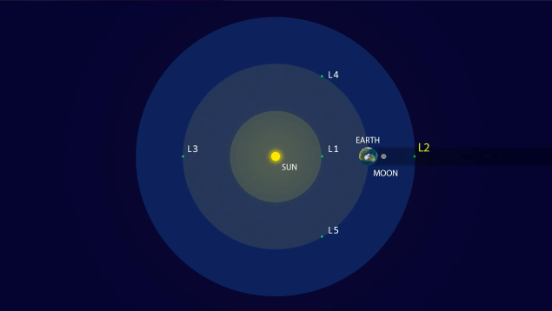
Satellite view from \( L_1 \)
ASSIGNMENT
- What is a Lagrangian Point?
- In the Sun-Earth system there are 5 Lagrangian points. How stable are they? Where are they located and why are there 5 of them?
GEOSTATIONARY ORBIT
There is a special orbit around a body where the periods of the central objects rotation and the orbiting bodies revolution match. This is a geostationary or geosynchronous orbit.
WHAT VELOCITY AND ALTITUDE IS REQUIRED FOR A GEOSTATIONARY ORBIT?
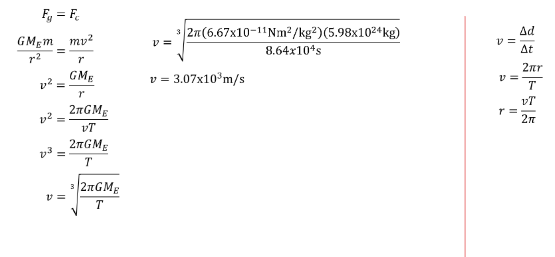
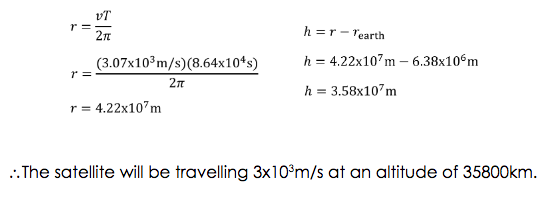
ARTIFICIAL GRAVITY

How fast is the ring spinning on the Discovery One? It has a radius of \( 6.0 m \) and let's assume that it generated a gravitational field of \( 1.6 m/s^2 \).
SOLUTION:
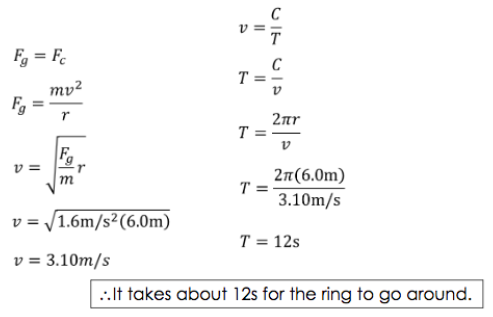
CORIOLIS FORCE
The Coriolis force is the reason that weather patterns always rotate the same direction in each hemisphere.
Sửa lần cuối: Thứ bảy, 10 Tháng 5 2025, 11:11 AM