Lesson 2.6 - Gravitational Potential Energy
VIDEO LESSON (21:05 min)
Video is not accessible in some countries. If you cannot view it, you might need VPN to do so.
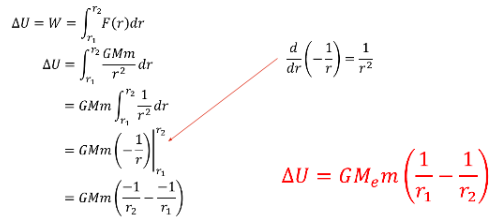


How can
Video is not accessible in some countries. If you cannot view it, you might need VPN to do so.
CONSIDER NEWTON'S UNIVERSAL GRAVITATION
If we consider an object of mass \( m \) on the surface of the earth, \( r_1=R_E \) is raised to a new altitude of \( r_2=R_E+h \). How much work is done to raise the object?
We know that it is acted on by a gravitational force given by the following formula.

Using the work formula
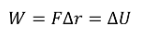
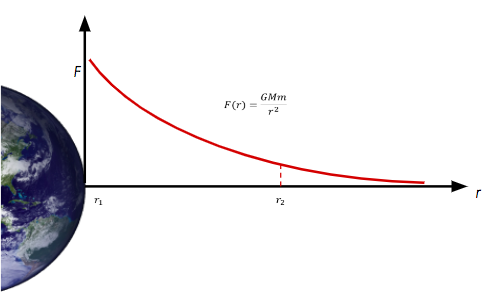
DERIVING GRAVITATIONAL POTENTIAL ENERGY (CALCULUS NONSENSE)
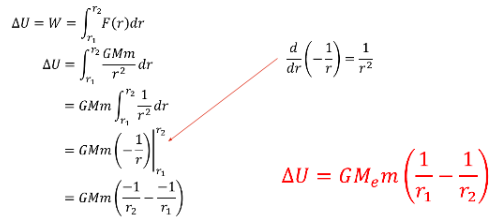
GRAVITATIONAL POTENTIAL ENERGY
Therefore the work required to move an object from \( r_1 \) to \( r_2 \) abover a planet with mass \( M \) (and thus the change in gravitational potential energy) is given by:
ESCAPE ENERGY
If we consider an object on the Earth it requires a certain amount of energy to be completely removed from the influence of Earth's gravitational pull. We need to go to a point infinitely far away from earth since the \( \vec{F}( \vec{r}) \rightarrow 0 \) as \( r \rightarrow \infty \).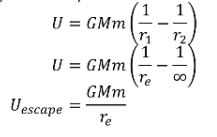
This is the energy required to escape the pull of Earth's gravity. We can call this the escape energy.
ESCAPE VELOCITY
To escape the pull of gravity we need to have enough kinetic energy to begin with to overcome this escape energy. Therefore
How can
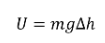
And
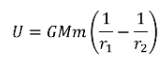
Are these equivalent for small changes in \( r \)? See if you can show that these are equivalent.
最后修改: 2025年05月19日 星期一 09:31