Lesson 2.7 - Orbital Energy
VIDEO LESSON (24:43 min)
Video is not accessible in some countries. If you cannot view it, you might need VPN to do so.

a) Kinetic energy
b) Total orbital energy
c) Binding energy
d) Escape velocity
e) Energy released if the satellite crashed into the Earth (neglect air resistance)
SOLUTION:

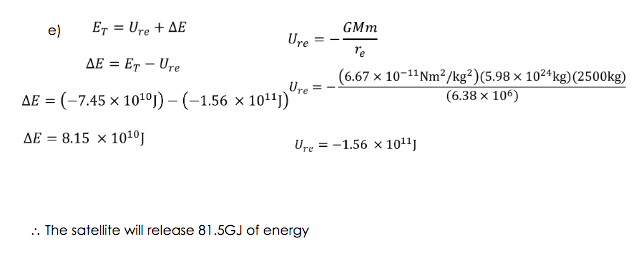
Video is not accessible in some countries. If you cannot view it, you might need VPN to do so.
GRAVITATIONAL POTENTIAL ENERGY
Recall: The energy required to move an object, m, in a gravitational field from \( r_1 \) to \( r_2 \) is given as
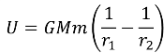
If we choose a reference point infinitely far away from the central mass
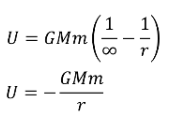
- When looking at potential energy the reference point is arbitrary.
- If we had used \( r = 0 \) as a reference point there would have been a singularity (divide by zero!) that would have caused problems.
- Consider an object infinitely far from a large mass (No potential energy). As it approaches the mass it gains kinetic energy, and thus speed, until it hits the mass or becomes bound in an orbit. Gravity is doing positive work as the mass approaches.
- This indicates a "bound state". It is bound until enough energy is added to the system to allow the object to escape.
ORBITAL KINETIC ENERGY
Now let's consider a satellite in orbits around the Earth. It has both kinetic and gravitational potential energy. Its gravitational force is equal to its centripetal force.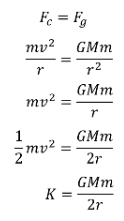
TOTAL ORBITAL ENERGY
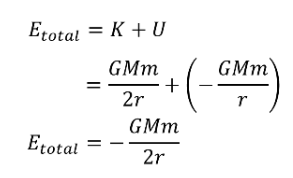
This represents the total energy of an orbiting satellite.
BINDING ENERGY
The energy required to free an orbiting mass is equal to the negative of the total energy.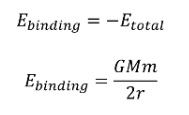
SUMMARY

EXAMPLE PROBLEM #1
A \( 2500 kg \) satellite is in orbit at \( 312 km \) above sea level. Determine its:a) Kinetic energy
b) Total orbital energy
c) Binding energy
d) Escape velocity
e) Energy released if the satellite crashed into the Earth (neglect air resistance)
SOLUTION:

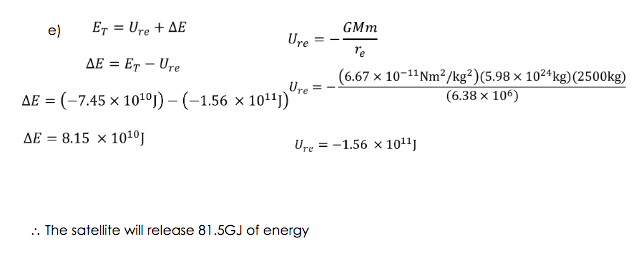
Last modified: Monday, 19 May 2025, 11:02 AM