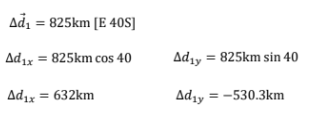Lesson 1.2 - Displacement and Velocity
By the end of this lesson, I will be able to:
Success Criteria:
By the end of this lesson, I can
VIDEO LESSON (45:41 min)
Video is not accessible in some countries. If you cannot view it, you might need VPN to do so.
RECALL
Displacement and velocity are vector quantities, i.e. they have magnitude and direction.
Displacement is the change in position, d, of an object with respect to a reference point in a given direction.
\( \Delta \vec{d} = 15m [W] \)
Velocity is the rate of change of position with respect to time.
\( \vec{v}=2.5m/s[Fwd]\)
Average velocity is the total displacement divided by time elapsed.
\(\vec{v}_{av}=\frac{\Delta \vec{d}}{\Delta t}\)
Watch Frames of Reference VIDEO (27:25 min)
Video is not accessible in some countries. If you cannot view it, you might need VPN to do so.
IN ONE DIMENSION
Once we define a frame of reference, we can just add vectors as if they were numbers.
EXAMPLE PROBLEM #1
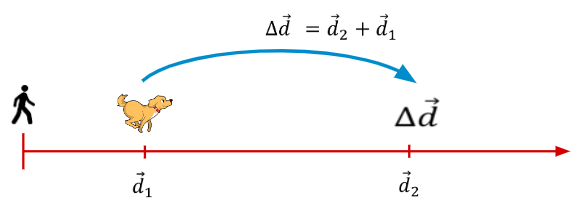
A dog initially 4.3 m away from you runs 12 m further away to fetch a stick. How far away is the dog after it gets the stick.
SOLUTION:
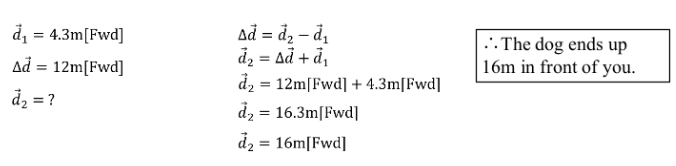
What if the dog ran the other direction?
SOLUTION:
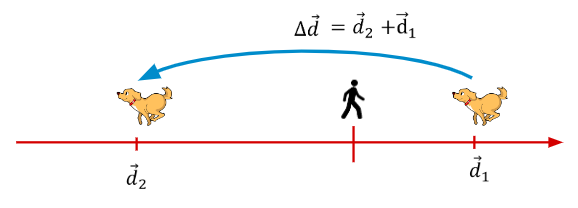

If the dog takes 0.4s, what are the velocities in each case?
SOLUTION:

IN TWO DIMENSIONS
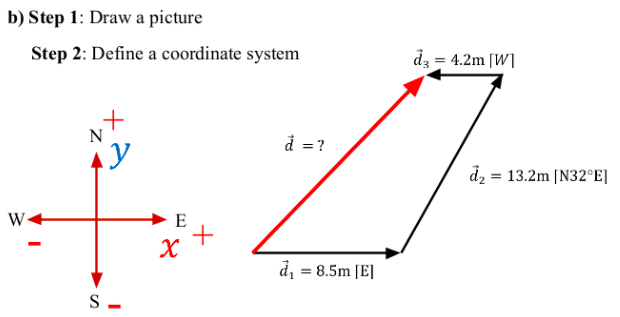
Step 1: Draw a picture
Step 2: Define a coordinate system
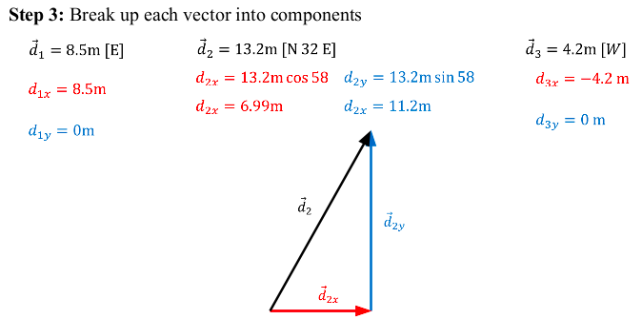
Step 3: Break up each vector into components
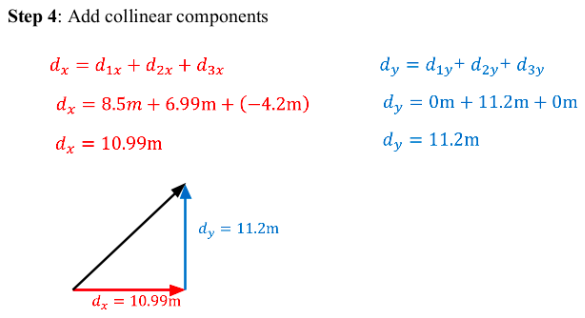
Step 4: Add collinear components
Step 5: Use Pythagorean Theorem and Trigonometry to determine magnitude and direction of the resultant vector
EXAMPLE PROBLEM #2
A wide receiver first runs \(8.5 m [E]\), then \(13.2 m [N 32^o E] \) when the ball is snapped and then \(4.2 m [W]\) before being tackled.a) Determine the total distance travelled and the wide receiver's average speed if this takes \(6.4s\)
b) Determine the total displacement and the wide receiver's average velocity.
SOLUTION:



You can proceed to solve Problem Set 1.2 now. Below are more examples.
EXAMPLE PROBLEM #3
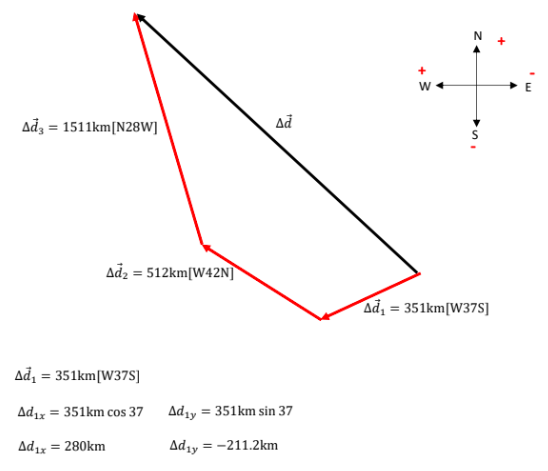
An airplane flies from Ottawa to Toronto, \(351 km [W 37^o S]\). Then it flies to Sault Ste. Marie, \(512 km [W 42^o N]\). Finally it flies to Churchill, Manitoba, \(1511 km [N 28^o W]\). What is the total displacement of the complete trip?SOLUTION:



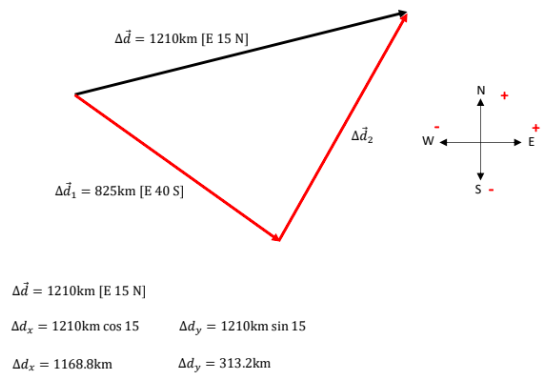
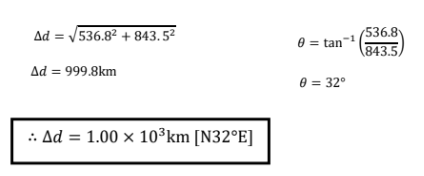
EXAMPLE PROBLEM #4
The total displacement of two flight is \(1210km[E 15^o N]\). If the first flight is \(825km [E 40^o S]\), determine the displacement of the second flight.SOLUTION: